Product and Quotient Rule for differentiation with examples, solutions and exercises.where, a≠ 0, log a AB = log a A + log a B Product Rule for Partial Derivatives: If we have a function z = f(x,y) g(x,y) and we want to find out the partial derivative of z, then we use the following formulaSolving Logarithmic Equations Generally, there are two types of logarithmic equations. Study each case carefully before you start looking at the worked examples below. Types of Logarithmic Equations The first type looks like this. If you have a single logarithm on each side of the equation having the same base then you can set the … Solving Logarithmic Equations Read More »★★★ Correct answer to the question: Which of the following illustrates the product rule for logarithmic equations? o log2 (4x) = log24+ log2 x log2(4x) = log24.log2 x log2(4x) = log24-log2x o log2(4x) = log24+log2 x - edu-answer.comKnow the product rule. The first property of logarithms, known as the "product rule," states that the logarithm of a multiplied product equals the sum of the logarithms of both factors. Written in equation form: logb(m * n) = logb(m) + logb(n)
Product Rule in Calculus (Definition, Formula, Proof
rule: logₐ(bc)=logₐb+logₐc; according to the rule: log₂(4x)=log₂4+log₂x Correct answer: D. log₂4+log₂xAnswers: 3, question: answers you are really se-xy :PStep-by-step explanation: Which of the following illustrates the product rule for logarithmic equations? log (4x) = log24 = log2x log2(4x) = log24-log2x o log2 (4x) = log24-log...So log base 2 of 4 times 8, is the log base 2 of 32. Now this is saying what power of 2 will give me 32. 2, 4, 8, 16, 32 fifth power. So what the product rule of logarithms is, is basically saying if we have 2 things inside of a log namely log base b of x times y times and by log base b, this holds for any base as long as the base is a positiveThe Product Rule for Logarithms Recall that we use the product rule of exponents to combine the product of like bases raised to exponents by adding the exponents: xaxb =xa+b x a x b = x a + b.

Solving Logarithmic Equations - ChiliMath
So I'm actually going to go and prove the product rule of logarithms for you so you can actually see that it's not some crazy mystery of a formula. So what I have is I have the product rule written up above and I have two claims, let m equal to log base b of x and n equal to log base b of y.We are given Logarithmic equations. We need to find the equation which illustrates the product rule. We know, the product rule of Logarithms is:. According to the product rule of Logarithms, we need to separate logs by plus sign. In the given options only 4th option logs are separated by plus sign.. Therefore, correct option is 4th option.Expand the logarithmic expression log(8) a/2. Login. Remember. Register; which expression is equivalent to the following complex fraction x/x-3/x^2/x^2-9. asked which of the following illustrates the product rule for logarithmic equations? asked Dec 3, 2020 in Other by manish56 (-32,547 points) 0 votes. 1 answer. what is the trueIn this section, you will: Use like bases to solve exponential equations. Use logarithms to solve exponential equations. Use the definition of a loga. = 3 Apply the product rule of logarithms. log 2 (6 x For the following exercises, use logarithms to solve.Define the Product Rule for Radicals. Define the Product Rule for Logarithms. Convert a Radical Expression to Exponential Form and Simplify. What are the three types of linear systems of linear equations? 1. Consistent 2. Inconsistent 3. Dependent. Rationalize 1/√3 ( 1 over the SqRt of 3 )
Recall that the logarithmic and exponential functions "undo" every different. This signifies that logarithms have equivalent houses to exponents. Some necessary houses of logarithms are given here. First, the following houses are easy to turn out.
[latex]\startcases\mathrmlog_b1=0\ \mathrmlog_bb=1\endinstances[/latex]For instance, [latex]\mathrmlog_51=0[/latex] since [latex]5^0=1[/latex]. And [latex]\mathrmlog_55=1[/latex] since [latex]5^1=5[/latex].
Next, now we have the inverse assets.
[latex]\startcases\hfill \ \mathrmlog_b\left(b^x\right)=x\hfill \ \textual content b^\mathrmlog_bx=x,x>0\hfill \endinstances[/latex]For example, to evaluate [latex]\mathrmlog\left(100\right)[/latex], we will be able to rewrite the logarithm as [latex]\mathrmlog_10\left(10^2\right)[/latex], and then observe the inverse assets [latex]\mathrmlog_b\left(b^x\right)=x[/latex] to get [latex]\mathrmlog_10\left(10^2\proper)=2[/latex].
To review [latex]e^\mathrmln\left(7\proper)[/latex], we will rewrite the logarithm as [latex]e^\mathrmlog_e7[/latex], after which observe the inverse property [latex]b^\mathrmlog_bx=x[/latex] to get [latex]e^\mathrmlog_e7=7[/latex].
Finally, we have the one-to-one belongings.
[latex]\mathrmlog_bM=\mathrmlog_bN\text if and only if\textual content M=N[/latex]We can use the one-to-one belongings to solve the equation [latex]\mathrmlog_3\left(3x\right)=\mathrmlog_3\left(2x+5\right)[/latex] for x. Since the bases are the same, we will apply the one-to-one belongings through environment the arguments equal and solving for x:
[latex]\begincircumstances3x=2x+5\hfill & \textual contentSet the arguments equal\textual content.\hfill \ x=5\hfill & \textual contentSubtract 2x\text.\hfill \endcases[/latex]But what about the equation [latex]\mathrmlog_3\left(3x\proper)+\mathrmlog_3\left(2x+5\proper)=2[/latex]? The one-to-one assets does now not assist us in this instance. Before we will be able to solve an equation like this, we want a technique for combining phrases on the left facet of the equation.
Recall that we use the product rule of exponents to mix the product of exponents through including: [latex]x^ax^b=x^a+b[/latex]. We have a similar assets for logarithms, known as the product rule for logarithms, which says that the logarithm of a product is equal to a sum of logarithms. Because logs are exponents, and we multiply like bases, we can add the exponents. We will use the inverse property to derive the product rule under.
Given any actual quantity x and sure actual numbers M, N, and b, where [latex]b\ne 1[/latex], we can display
[latex]\mathrmlog_b\left(MN\right)\textual content=\mathrmlog_b\left(M\proper)+\mathrmlog_b\left(N\right)[/latex].Let [latex]m=\mathrmlog_bM[/latex] and [latex]n=\mathrmlog_bN[/latex]. In exponential shape, these equations are [latex]b^m=M[/latex] and [latex]b^n=N[/latex]. It follows that
[latex]\begininstances\mathrmlog_b\left(MN\proper)\hfill & =\mathrmlog_b\left(b^mb^n\proper)\hfill & \textual contentSubstitute for M\textual content and N.\hfill \ \hfill & =\mathrmlog_b\left(b^m+n\right)\hfill & \textual contentApply the product rule for exponents.\hfill \ \hfill & =m+n\hfill & \textApply the inverse assets of logs.\hfill \ \hfill & =\mathrmlog_b\left(M\right)+\mathrmlog_b\left(N\proper)\hfill & \textual contentSubstitute for m\textual content and n.\hfill \finishcases[/latex]Note that repeated applications of the product rule for logarithms let us simplify the logarithm of the product of any quantity of factors. For instance, believe [latex]\mathrmlog_b\left(wxyz\proper)[/latex]. Using the product rule for logarithms, we can rewrite this logarithm of a product as the sum of logarithms of its elements:
[latex]\mathrmlog_b\left(wxyz\right)=\mathrmlog_bw+\mathrmlog_bx+\mathrmlog_by+\mathrmlog_bz[/latex] A General Note: The Product Rule for LogarithmsThe product rule for logarithms can be used to simplify a logarithm of a product by way of rewriting it as a sum of person logarithms.
[latex]\mathrmlog_b\left(MN\proper)=\mathrmlog_b\left(M\proper)+\mathrmlog_b\left(N\right)\textual content for b>0[/latex] How To: Given the logarithm of a product, use the product rule of logarithms to write down an equivalent sum of logarithms. Factor the argument utterly, expressing each and every whole quantity issue as a product of primes. Write the similar expression by way of summing the logarithms of each issue. Example 1: Using the Product Rule for LogarithmsExpand [latex]\mathrmlog_3\left(30x\left(3x+4\proper)\proper)[/latex].
SolutionWe begin through factoring the argument completely, expressing 30 as a product of primes.
[latex]\mathrmlog_3\left(30x\left(3x+4\right)\right)=\mathrmlog_3\left(2\cdot 3\cdot 5\cdot x\cdot \left(3x+4\proper)\proper)[/latex]Next we write the an identical equation through summing the logarithms of each factor.
[latex]\mathrmlog_3\left(30x\left(3x+4\proper)\proper)=\mathrmlog_3\left(2\right)+\mathrmlog_3\left(3\proper)+\mathrmlog_3\left(5\proper)+\mathrmlog_3\left(x\proper)+\mathrmlog_3\left(3x+4\proper)[/latex] Try It 1Expand [latex]\mathrmlog_b\left(8k\proper)[/latex].
Solution
Product and quotient rule - Free math help

Solved: Solve the following problems using the MATLAB ...

Simplifying radical expressions, rational exponents ...

Logarithm rules pdf

Expanding Logarithms - ChiliMath
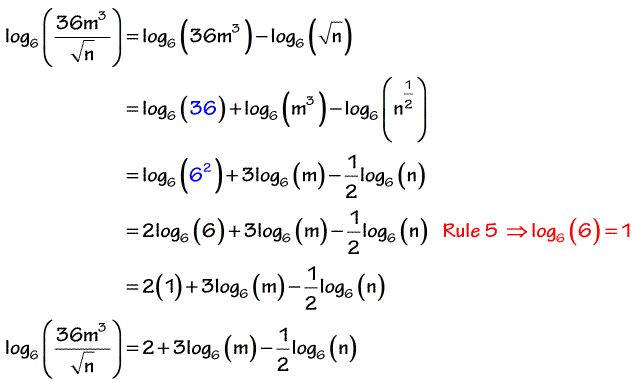
!!15 points!!! Antifreeze is added to a car's radiator to ...

How to Use a Logarithmic Differentiation to Find the ...

Product and quotient rule - Free math help

Advanced Math Archive | June 20, 2017 | Chegg.com
PPT - Unit 5: Modeling with Exponential & Logarithmic ...

Product and quotient rule - Free math help

How to Solve Log Equations: Algebra 2/Trig. - MathSux^2

Log Functions #trigonometry | Exponential and Logarithmic ...

Solving Exponential and Logarithmic Equations | CK-12 ...

Logarithm properties review (article) | Khan Academy
Product and quotient rule - Free math help

3 Ways to Solve Logarithms - wikiHow

Log Rules and Formulas | Logarithmic Equations, Special ...

Solving Equations by Distributive Property (solutions ...

Product and quotient rule - Free math help

Logarithms - Product Rule (solutions, examples, videos ...

0 comments:
Post a Comment